ปริมาณสารสัมพันธ์
ปริมาณสารสัมพันธ์ คือ ความสัมพันธ์ระหว่างมวลหรือน้ำหนักของธาตุต่าง ๆ ของสารประกอบในปฏิกิริยาเคมี ปริมาณสารสัมพันธ์มีประโยชน์ในแง่ของการคาดคะเนปริมาณของสารที่ต้องใช้เป็นสารตั้งต้นเพื่อให้เกิดผลิตภัณฑ์ที่ต้องการ
ระบบเปิดระบบปิด
ระบบ ( System) หมายถึง สิ่งซึ่งอยู่ในขอบเขตที่ศึกษา
ระบบเปิด (Open System) หมายถึง ระบบที่มีการถ่ายเทมวลของสารระหว่างระบบกับสิ่งแวดล้อมหรือระบบ ซึ่งมวลและพลังงานของสารก่อนการเปลี่ยนแปลงและหลังการเปลี่ยนแปลงมีค่าไม่คงที่ เช่น
ระบบเปิด (Open System) หมายถึง ระบบที่มีการถ่ายเทมวลของสารระหว่างระบบกับสิ่งแวดล้อมหรือระบบ ซึ่งมวลและพลังงานของสารก่อนการเปลี่ยนแปลงและหลังการเปลี่ยนแปลงมีค่าไม่คงที่ เช่น
ระบบปิด ( Closed System) หมายถึงระบบที่ไม่มีการถ่ายเทมวลสารกับสิ่งแวดล้อมหรือระบบ ซึ่งมวลของสารก่อนการเปลี่ยนแปลง และหลังการเปลี่ยนแปลงคงที่ แต่พลังงานของสารก่อนการเปลี่ยนแปลงและหลังการเปลี่ยนแปลงไม่คงที่ เช่น
กฎต่าง ๆ ที่เกี่ยวข้องกับการเปลี่ยนแปลง
1. กฎทรงมวล
อองตวน โลรอง ลาวัวซิเอ ได้ตั้งกฎทรงมวลซึ่งสรุปได้ว่า “มวลของสารทั้งหมดก่อนทำปฏิกิริยาย่อมเท่ากับมวลของสารทั้งหมดหลังทำปฏิกิริยา” กฎนี้จะใช้ได้กับปฏิกิริยาเคมีในระบบปิด ใช้ไม่ได้กับปฏิกิริยาเคมีนิวเคลียร์ เช่น เทียนไขในภาชนะปิดใบหนึ่ง มวลของสารทั้งหมดก่อนทำปฏิกิริยาเท่ากับมวลของเทียนไขกับภาชนะ เมื่อจุดเทียนไขในภาชนะปิดนี้ แล้วทำการชั่งมวลใหม่ มวลจะเท่าเดิม (ระบบปิด)
2. กฎสัดส่วนคงที่
โจเซฟ เพราสต์ ได้ตั้งกฎสัดส่วนคงที่ซึ่งสรุปได้ว่า “ในสารประกอบหนึ่ง ๆ ธาตุต่าง ๆ ที่เป็นองค์ประกอบรวมตัวกันด้วยอัตราส่วนโดยน้ำหนักที่คงที่เสมอ” โดยไม่คำนึงถึงว่าสารประกอบนั้นจะมีกำเนิดหรือเตรียมได้โดยวิธีใด
มวลอะตอม
อะตอมเป็นอนุภาคที่เล็กที่สุดของธาตุที่สามารถทำปฏิกิริยาเคมีได้ มีรัศมีของอะตอมยาวประมาณ 10 -10 เมตร อะตอมที่เบาที่สุดมีมวลประมาณ 1.6 x 10 -24 กรัม อะตอมที่หนักที่สุดมีมวลประมาณ 250 เท่า ซึ่งมีค่าน้อยมาก (เป็นผลคูณของ 10 -24) มวลอะตอมเหล่านี้จะต้องรวมกันต่อไปเป็นมวลโมเลกุล ซึ่งทำให้ยุ่งยากในการคำนวณ จึงนิยมใช้มวลเปรียบเทียบที่เรียกว่า มวลอะตอมหรือน้ำหนักอะตอม
มวลของอะตอมนั้นก็คือ มวลขององค์ประกอบทั้งหมดในอะตอมรวมกัน อันได้แก่ โปรตอน นิวตรอน และอิเล็กตรอน ซึ่งมวลของโปรตอน และนิวตรอนนั้นใกล้เคียงกันมาก แต่ไม่เท่ากัน และสูงกว่าอิเล็กตรอน นับพันเท่า
อนุภาค
|
มวล ( กรัม)
|
โปรตอน
|
1.6726 x 10 -24
|
นิวตรอน
|
1.6749 x 10 -24
|
อิเล็กตรอน
|
9.1096 x 10 -28
|
มวลอะตอม คือ มวลเปรียบเทียบที่บอกให้ทราบว่ามวลของธาตุ 1 อะตอมหนักเป็นกี่เท่าของมวลของธาตุมาตรฐาน 1 อะตอม
มวลของธาตุ 1 อะตอม คือ มวลที่แท้จริงของอะตอมนั้นๆ 1 อะตอม
มวลของธาตุมาตรฐาน 1 อะตอม คือ มวลของธาตุที่ถูกใช้เป็นตัวเปรียบเทียบ ซึ่งทุกอะตอมต้องมีค่าเท่ากันหมด จึงเรียกว่ามวลมาตรฐาน มีค่าเท่ากับ 1.66 x 10 -24 กรัม หรือ 1 amu (atomic mass unit)
ถ้ามวลอะตอมของ C = 12 จากสูตรการหามวลอะตอมของธาตุ มวลของธาตุ C 1 อะตอม = 12 x 1.66 x 10 -24 กรัม ถ้าใช้มวลของธาตุ C 1 อะตอมเป็นค่ามาตรฐานจะได้สูตร

นอกจากนี้มวลอะตอมยังคำนวณได้จากมวลเฉลี่ยของบรรดาไอโซโทปที่มีในธรรมชาติ

ลักษณะสำคัญของมวลอะตอม มีดังนี้
1. มวลอะตอมของธาตุไม่มีหน่วย
2. มวลอะตอมเป็นค่าเปรียบเทียบ ส่วนมวลของธาตุ 1 อะตอมเป็นมวลที่แท้จริง มีหน่วยเป็นกรัม
3. มวลของธาตุมาตรฐาน 1 อะตอม ที่ใช้เป็นตัวถูกเปรียบเทียบของมวลอะตอมมีค่าเท่ากันหมดในทุก ๆ ธาตุ
4. คำนวณได้จากสูตรเมื่อทราบมวลของธาตุนั้น 1 อะตอม และคำนวณได้จากไอโซโทปของธาตุนั้น ๆ
มวลโมเลกุล
เนื่องจากโมเลกุลมีขนาดเล็กมากเช่นเดียวกับอะตอม ดังนั้น มวลของโมเลกุลจึงนิยมบอกเป็นค่าเปรียบเทียบเช่นกัน
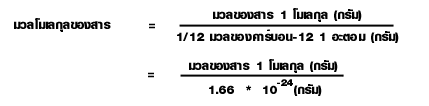
ลักษณะสำคัญของมวลโมเลกุล
1. มวลโมเลกุลไม่มีหน่วย เพราะเป็นค่าเปรียบเทียบกับค่ามาตรฐาน
2. มวลของสาร 1 โมเลกุล คือมวลที่แท้จริงของโมเลกุลนั้น ๆ 1 โมเลกุล
3. มวลโมเลกุลคำนวณได้จากมวลอะตอมรวมกัน เพราะโมเลกุลเกิดจากอะตอมรวมกัน หรือได้จากมวลของสาร 1 โมเลกุล เปรียบเทียบค่ามาตรฐาน
4. มวลมาตรฐานที่ถูกเปรียบเทียบต้องมีค่าเท่ากันหมดในทุก ๆ โมเลกุล
2. มวลของสาร 1 โมเลกุล คือมวลที่แท้จริงของโมเลกุลนั้น ๆ 1 โมเลกุล
3. มวลโมเลกุลคำนวณได้จากมวลอะตอมรวมกัน เพราะโมเลกุลเกิดจากอะตอมรวมกัน หรือได้จากมวลของสาร 1 โมเลกุล เปรียบเทียบค่ามาตรฐาน
4. มวลมาตรฐานที่ถูกเปรียบเทียบต้องมีค่าเท่ากันหมดในทุก ๆ โมเลกุล
การคำนวณมวลโมเลกุลของสาร
ตัวอย่าง จงหามวลโมเลกุลของ CaSO 4 . 2H 2O กำหนดมวลอะตอมของ Ca = 40, S = 32, O = 16 และ H = 1
วิธีทำ มวลโมเลกุลของ CaSO 4 . 2H 2O = มวลอะตอมของทุกธาตุใน CaSO 4 . 2H 2O รวมกัน
= 40+32+(16 x 4)+2(2)+2(16)
= 40+32+64+4+32 = 172
ดังนั้น มวลโมเลกุลของ CaSO 4 . 2H 2O = 172 ตอบ
โมล
โมล คือ หน่วยของปริมาณสารหน่วยหนึ่งที่มีความหมายเช่นเดียวกับกรัมโมเลกุล กรัมอะตอมหรือกรัมไอออน มีวิธีหาได้ 4 แบบ ดังต่อไปนี้
1. จำนวนอนุภาคต่อโมลของสาร
สสารทุกชนิด 1 โมลมีจำนวน 6.023 x 10 23 อนุภาค (6.023 x 10 23 คือเลขอาโวกาโดร)
อนุภาค คือ อะตอมโมเลกุล ไอออน อิเล็กตรอน เป็นต้น
- ธาตุ เช่น Na 1 โมล มีจำนวน 6.023 x 10 23 โมเลกุล หรือ 6.023 x 10 23 อะตอม Na + 1 โมล มีจำนวน 6.023 x 10 23 ไอออน
Cl 2 1 โมล มีจำนวน 6.023 x 10 23 โมเลกุล หรือ 2 x 6.023 x 10 23 อะตอม ( 1 โมเลกุลมี 2 อะตอม),
Cl - 1 โมล มีจำนวน 6.023 x 10 23 ไอออน
- สารประกอบ เช่น SO 3 1 โมล มีจำนวน 6.023 x 10 23 โมเลกุล หรือ 4 x 6.023 x 10 23 อะตอม (SO 3 1 โมเลกุลประกอบด้วย H 2 อะตอม S 1 อะตอม และ O 4 อะตอม รวมเป็น 7 อะตอม)
2. จำนวนโมลกับมวลของสาร
โมล = มวลสาร / มวลอะตอมหรือมวลโมเลกุล
มวลโมเลกุลหรือมวลอะตอม = มวล( กรัม)
มวลโมเลกุลหรือมวลอะตอม = มวล( กรัม)
ดังนั้น มวลหรือน้ำหนักของสาร 1 โมล คือมวลโมเลกุลหรือมวลอะตอม ตัวอย่าง เช่น O 2 1 โมล หนัก 32 กรัม จงหามวลโมเลกุลของก๊าซออกซิเจน เมื่อกำหนดให้มวลอะตอมของ O = 16
1 โมล = 32 / มวลโมเลกุลของก๊าซออกซิเจน
มวลโมเลกุลของก๊าซออกซิเจน = 32 g
ดังนั้น มวลโมเลกุลของก๊าซออกซิเจน = 32
จะเห็นว่ามวลโมเลกุลของก๊าซออกซิเจนมีค่าเท่ากับน้ำหนักของก๊าซออกซิเจน
3. ปริมาตรต่อโมลของก๊าซ
ก๊าซทุกชนิด 1 โมล มี 22.4 ลูกบาศก์เซนติเมตรที่ STP คือที่อุณหภูมิและความดันมาตรฐาน ( ที่ 0 องศาเซลเซียส 1 บรรยากาศ หรือ 273 เคลวิน 760 มิลลิเมตรของปรอท)
ตัวอย่าง เช่น ไอน้ำ 1 โมล มีปริมาตร 22.4 ลูกบาศก์เดซิเมตร ที่ STP
ความสัมพันธ์ระหว่างจำนวนโมล อนุภาค มวล และปริมาตร
สาร 1 โมลจะมีมวลเป็นกรัมเท่ากับมวลอะตอมและมีจำนวนอนุภาคเท่ากับ 6.023 x 10 23 อนุภาค และถ้าสารนั้น เป็นก๊าซที่ STP จะมีปริมาตรเท่ากับ 22.4 ลูกบาศก์เดซิเมตร

ตัวอย่าง จงหาปริมาตรที่ STP ของก๊าซไฮโดรเจนคลอไรด์ (HCl) 7.3 กรัม
โมล = 7.3 g / 36.5 g = 0.2
ก๊าซ HCl 1 โมล มีปริมาตร 22.4 dm 3 ที่ STP
ก๊าซ HCl 0.2 โมล มีปริมาตร 22.4 x 0.2 = 4.48 dm 3 ที่ STP
ดังนั้น ก๊าซไฮโดรเจนคลอไรด์ 7.3 g มีปริมาตร 4.48 dm 3 ที่ STP
4. กฎของอาโวกาโดร
โมลของก๊าซหาได้จากกฎของอาโวกาโดร กฎของอาโวกาโดรสรุปว่า “ ภายใต้เงื่อนไขเดียวกัน ( อุณหภูมิและความดัน) ก๊าซทุกชนิดที่มีปริมาตรเท่ากันจะมีจำนวนโมเลกุลและจำนวนโมลเท่ากัน เช่น ก๊าซออกซิเจน 1 ลูกบาศก์เดซิเมตร จะมีจำนวน โมลและโมเลกุลเท่ากับก๊าซไฮโดรเจน 1 ลูกบาศก์เดซิเมตร ที่อุณหภูมิและความดันเดียวกัน และยังเท่ากับจำนวนโมลและโมเลกุลชองก๊าซอื่น ๆ ที่มีปริมาตรเท่ากันภายใต้อุณหภูมิและความดันเดียวกัน
ตัวอย่าง ที่สภาวะมาตรฐาน ก๊าซออกซิเจน 1 ลูกบาศก์เดซิเมตร หนัก 1.43 กรัม และก๊าซคาร์บอนมอนอกไซด์ 1 ลูกบาศก์เดซิเมตร หนัก 1.25 กรัม จงหามวลโมเลกุลของก๊าซคาร์บอนมอนอกไซด์
วิธีทำ จากกฎของอาโวกาโดร ก๊าซออกซิเจนและก๊าซคาร์บอนมอนอกไซด์มีปริมาตรเท่ากันที่สภาวะมาตรฐานเหมือนกัน มีจำนวนโมลและโมเลกุลเท่ากัน
จำนวนโมลของก๊าซคาร์บอนมอนอกไซด์ = จำนวนโมลของก๊าซออกซิเจน
1.25 / a = 1.43 / 16
a = 28
ดังนั้น มวลโมเลกุลของก๊าซคาร์บอนมอนอกไซด์ = 28 ตอบ
1.25 / a = 1.43 / 16
a = 28
ดังนั้น มวลโมเลกุลของก๊าซคาร์บอนมอนอกไซด์ = 28 ตอบ
สูตรเคมีและสมการเคมี
จำนวนโมลหาได้จากกฎของเกย์- ลูสแซกและกฎของอาโวกาโดร การหาจำนวนโมลโดยวิธีนี้เป็นการหาจำนวนโมลของสมการเคมี กฎของเกย์- ลูสแซกสรุปว่า “ปริมาตรของก๊าซที่ทำปฏิกิริยากันและที่ได้จากปฏิกิริยาจะเป็นอัตราส่วนลงตัวน้อย ๆ ที่อุณหภูมิและความดันเดียวกัน”
ตัวอย่าง เช่น ก๊าซไนโตรเจน (N 2) 10 ลูกบาศก์เดซิเมตร ทำปฏิกิริยาพอดีกับก๊าซไฮโดรเจน (H 2) 30 ลูกบาศก์เดซิเมตรจะเกิดก๊าซแอมโมเนีย (NH 3) 20 ลูกบาศก์เดซิเมตร
N 2(g) + 3H 2(g) ------> 2NH 3(g)
10 ...........30................. 20 dm 3 กฎของเกย์- ลูสแซก
1 ..............3 ..................2 dm 3 ( ที่อุณหภูมิและความดันเดียวกัน)
จากกฎของอาโวกาโดร : ที่อุณหภูมิและความดันเดียวกัน
ถ้า N 2(g) 1 dm 3 คิดเป็น 1 โมลหรือ 1 โมเลกุล
H 2(g) 1 dm 3 คิดเป็น 1 โมลหรือ 1 โมเลกุล
H 2(g) 3 dm 3 คิดเป็น 3 โมลหรือ 3 โมเลกุล
NH 3 1 dm 3 คิดเป็น 1 โมลหรือ 1 โมเลกุล
NH 3(g) 2 dm 3 คิดเป็น 2 โมลหรือ 2โมเลกุล
N 2(g) + 3H 2(g) ------> 2NH 3(g)
1 .............3.................... 2 โมล ( โมเลกุล) กฎของอาโวกาโดร ( ที่อุณหภูมิและความดันเดียวกัน)
จากกฎของเกย์- ลูกแซกและกฎของอาโวกาโดร สรุปได้ว่า อัตราส่วนอย่างต่ำ ( โดยปริมาตร) ของก๊าซที่เข้าทำปฏิกิริยากันและที่ได้จากปฏิกิริยาจะเท่ากับจำนวนโมลหรือจำนวนโมเลกุลของก๊าซนั้น
ลักษณะสำคัญของกฎของเกย์- ลูสแซกและกฎของอาโวกาโดร
1. จำนวนโมลและโมเลกุลของสมการเคมีจะมีค่าเท่ากับปริมาตรของก๊าซที่เข้าทำปฏิกิริยาพอดีกันนั่นเอง
2. จำนวนโมลเหล่านี้คือตัวเลขที่ใช้ในการดุลสมการเคมี เช่น 4NH 3(g) +3O 2(g) 2N 2(g)+6H 2O(g)
2N 2(g)+6H 2O(g)
3. จากปริมาตรของก๊าซที่ทำปฏิกิริยาพอดีกันและที่ได้จากปฏิกิริยาที่อุณหภูมิและความดันเดียวกัน สามารถนำไปใช้หาสูตรโมเลกุลของก๊าซได้ โดยอาศัยหลักการดุลสมการเคมี
2. จำนวนโมลเหล่านี้คือตัวเลขที่ใช้ในการดุลสมการเคมี เช่น 4NH 3(g) +3O 2(g)
3. จากปริมาตรของก๊าซที่ทำปฏิกิริยาพอดีกันและที่ได้จากปฏิกิริยาที่อุณหภูมิและความดันเดียวกัน สามารถนำไปใช้หาสูตรโมเลกุลของก๊าซได้ โดยอาศัยหลักการดุลสมการเคมี
ตัวอย่าง ก๊าซ X 15 ลูกบาศก์เซนติเมตร ทำปฏิกิริยาพอดีกับก๊าซ Y 45 ลูกบาศก์เซนติเมตร เกิดก๊าซ Z เพียงอย่างเดียว 30 ลูกบาศก์เซนติเมตร ปริมาตรของก๊าซทั้งหมดวัดที่อุณหภูมิและความดันเดียวกัน จงหาสูตรโมเลกุลของก๊าซ Z
วิธีทำ เมื่อก๊าซ X และ Y ทำปฏิกิริยากันได้ก๊าซ Z เพียงอย่างเดียว ดังนั้น ก๊าซ Z จะต้องมีธาตุ X และ Y เป็นองค์ประกอบ ดังสมการ
X 2(g) + Y 2(g)X aY b(Z)
15 .........45.............. 30 cm 3 ( จากกฎเกย์- ลูสแซก)
1 ...........3................ 2 cm 3 ( ที่อุณหภูมิและความดันเดียวกัน)
1 ...........3................ 2 mol ( จากกฎอาโวกาโดร ที่อุณหภูมิและ ความดันเดียวกัน) 1X 2(g) + 3Y 2(g)2 X aY b
เมื่อดุลสมการเคมี จำนวนอะตอมทั้ง 2 ข้างต้องเท่ากัน a = 1, b = 3
ดังนั้น สูตรของ Z คือ XY 3 ตอบ
4. จากสมการแสดงปฏิกิริยาเคมีของก๊าซที่ดุลแล้ว อัตราส่วนจำนวนโมลหรือจำนวนโมเลกุลจะเท่ากับอัตราส่วนโดยปริมาตรของก๊าซที่เข้าทำปฏิกิริยากันและที่ได้จากปฏิกิริยา สามารถนำไปใช้หาปริมาตรของก๊าซต่าง ๆ ในปฏิกิริยาเคมีนั้น ๆ ได้
ตัวอย่าง ก๊าซผสมระหว่างก๊าซมีเทน (CH 4) กับก๊าซโพรเพน (C 3H 8) อย่างละ 15 ลูกบาศก์เซนติเมตร จะต้องใช้ก๊าซออกซิเจนกี่ลูกบาศก์เซนติเมตรจึงจะทำปฏิกิริยาพอดีกับก๊าซผสมนี้ กำหนดสมการเคมีของปฏิกิริยาเคมีดังนี้
CH 4(g) + O 2(g) ---------> H 2O(g) + CO 2(g) …………..(1)
C 3H 8(g) + O 2(g) ----------> H 2O(g) + CO 2(g) …………..(2)
C 3H 8(g) + O 2(g) ----------> H 2O(g) + CO 2(g) …………..(2)
วิธีทำ จากสมการ (1) ดุลสมการได้ดังนี้
CH 4(g) + 2O 2(g)2H 2O( ) + CO 2(g)
1 ..............2.................... 2............. 1 mol กฎอาโวกาโดร
1 ..............2 ....................2 .............1 mol และกฎเกย์- ลูสแซกCH 4 1 cm 3 ทำปฏิกิริยาพอดีกับก๊าซออกซิเจน = 2 cm 3
CH 4 15 cm 3 ทำปฏิกิริยาพอดีกับก๊าซออกซิเจน = 15 x 2 = 30 cm 3
จาก (2) ;
C 3H 8(g) + 5O 2(g)4H 2O(g) + 3CO 2(g)
1 ..................5 ....................4 ..............3 mol
1 ..................5 ....................4 ..............3 cm 3
C 3H 8 1 cm 3 ทำปฏิกิริยาพอดีกับก๊าซออกซิเจน = 5 cm 3
C 3H 8 15 cm 3 ทำปฏิกิริยาพอดีกับก๊าซออกซิเจน = 15 x 5 = 75 cm 3
ต้องใช้ก๊าซออกซิเจนทั้งหมด = 30 = 75 = 105 cm 3 ตอบ
การหาสูตรเอมพิริคัลของสาร
สูตรเอมพิริคัล เป็นสูตรที่แสดงอัตราส่วนอย่างต่ำของธาตุองค์ประกอบ เช่น ไฮโดรเจนเปอร์ออกไซด์มีสูตรโมเลกุลเป็น H 2O 2 อัตราส่วนอย่างต่ำของจำนวนอะตอม H : O เท่ากับ 1 : 1 สูตรเอมพิริคัลจึงเป็น HO กลูโคสมีสูตรโมเลกุลเป็น C 6H 12O 6 อัตราส่วนอย่างต่ำของจำนวนอะตอม C : H : O เท่ากับ 1 : 2 : 1 สูตรเอมพิริคัลจึงเป็น CH 2O
การหาสูตรเอมพิริคัล มีหลักดังนี้
1. ต้องทราบว่าสารที่จะหาสูตรเอมพิริคัลประกอบด้วยธาตุใดบ้าง
2. ต้องทราบมวลอะตอมของแต่ละธาตุในสารที่จะหาสูตรเอาพิริคัล
3. ต้องทราบมวลของแต่ละธาตุในสารที่จะหาสูตร
4. ให้ข้อมูลจากข้อ 1, 2 และ 3 หาอัตราส่วนโดยโมล ด้วยการนำมวลของแต่ละธาตุหารด้วยมวลอะตอมของมันมาเข้าอัตราส่วน
5. สำหรับการปัดจุดทศนิยมของตัวเลขในการหาอัตราส่วนโดยโมล โดยทำตัวเลขใดตัวเลขหนึ่ง ให้เป็น 1 แล้วจึงปัดจุดทศนิยมด้วยวิธีปัด 0.1 - 0.2 ทิ้ง ถ้าเป็น 0.8 - 0.9 ปัดขึ้นอีก 1 ถ้าเป็น 0.0 - 0.7 ปัดไม่ได้ต้องหาตัวเลขที่ต่ำที่สุดมาคูณตัวเลขของอัตราส่วนโดยโมลให้มีค่าใกล้กับที่ จะปัดจุดทศนิยมได้ แล้วปัดจุดทศนิยมตัวเลขให้เป็นจำนวนเต็ม อนึ่งการปัดจุดทศนิยม ถ้าตัวเลขปัดจุดทศนิยมไม่ได้ ตัวเลขทุกตัวของอัตราส่วนโดยโมลนั้นก็จะไม่ปัดจุดทศนิยม หาตัวเลขมาคูณให้ได้ตัวเลขที่จะปัดจุดทศนิยมได้อัตราส่วนโดยโมลที่เป็นจำนวนเต็มได้สูตรเอมพิริคัล
2. ต้องทราบมวลอะตอมของแต่ละธาตุในสารที่จะหาสูตรเอาพิริคัล
3. ต้องทราบมวลของแต่ละธาตุในสารที่จะหาสูตร
4. ให้ข้อมูลจากข้อ 1, 2 และ 3 หาอัตราส่วนโดยโมล ด้วยการนำมวลของแต่ละธาตุหารด้วยมวลอะตอมของมันมาเข้าอัตราส่วน
5. สำหรับการปัดจุดทศนิยมของตัวเลขในการหาอัตราส่วนโดยโมล โดยทำตัวเลขใดตัวเลขหนึ่ง ให้เป็น 1 แล้วจึงปัดจุดทศนิยมด้วยวิธีปัด 0.1 - 0.2 ทิ้ง ถ้าเป็น 0.8 - 0.9 ปัดขึ้นอีก 1 ถ้าเป็น 0.0 - 0.7 ปัดไม่ได้ต้องหาตัวเลขที่ต่ำที่สุดมาคูณตัวเลขของอัตราส่วนโดยโมลให้มีค่าใกล้กับที่ จะปัดจุดทศนิยมได้ แล้วปัดจุดทศนิยมตัวเลขให้เป็นจำนวนเต็ม อนึ่งการปัดจุดทศนิยม ถ้าตัวเลขปัดจุดทศนิยมไม่ได้ ตัวเลขทุกตัวของอัตราส่วนโดยโมลนั้นก็จะไม่ปัดจุดทศนิยม หาตัวเลขมาคูณให้ได้ตัวเลขที่จะปัดจุดทศนิยมได้อัตราส่วนโดยโมลที่เป็นจำนวนเต็มได้สูตรเอมพิริคัล
สารกำหนดปริมาณและร้อยละของผลได้ของสารผลิตภัณฑ์
สารกำหนดปริมาณ ( Limiting Reagent)
สารที่เข้าทำปฏิกิริยามีปริมาณไม่พอดีกัน ปฏิกิริยาที่เกิดขึ้นจะสิ้นสุดเมื่อสารใดสารหนึ่งหมด สาร ที่หมดก่อนจะเป็นตัวกำหนดปริมาณของผลิตภัณฑ์ของสารผลิตภัณฑ์ที่เกิดขึ้นเรียกว่า สารกำหนดปริมาณ ( Limiting Reagent)
สารกำหนดปริมาณในการเกิดปฏิกิริยาเป็นการคำนวณสารจากสมการของปฏิกิริยาที่โจทย์บอกข้อมูลเกี่ยวกับสารตั้งต้นมาให้มากกว่าหนึ่งชนิด ลักษณะโจทย์มี 2 แบบ คือ
1. โจทย์บอกข้อมูลของสารตั้งต้นมาให้มากกว่าหนึ่งชนิด แต่ไม่บอกข้อมูลเกี่ยวกับสารผลิตภัณฑ์ ในการคำนวณต้องพิจารณา ว่าสารใดถูกใช้ทำปฏิกิริยาหมด แล้วจึงใช้สารนั้นเป็นหลักในการคำนวณสิ่งที่ต้องการจากสมการได้
2. โจทย์บอกข้อมูลของสารตั้งต้นมาให้มากกว่าหนึ่งชนิด และบอกข้อมูลของสารผลิตภัณฑ์ชนิด ใดชนิดหนึ่งมาให้ด้วย ในการคำนวณให้ใช้ข้อมูลจากสารผลิตภัณฑ์เป็นเกณฑ์ในการเทียบหาสิ่งที่ต้องการจากสมการเคมี
ร้อยละของผลได้ของสารผลิตภัณฑ์
ในการคำนวณหาปริมาณของผลิตภัณฑ์จากสมการเคมีนั้น ค่าที่ได้เรียกว่า ผลได้ตามทฤษฎี ( Theoretical yield) แต่ในทางปฏิบัติจะได้ผลิตภัณฑ์น้อยกว่าตามทฤษฎี แต่จะได้มากหรือน้อยแค่ไหน ก็ขึ้นอยู่กับวิธีการและสารเคมีที่ใช้ เรียกผลที่ได้ว่านี้ ผลได้จริง ( Actual yield) สำหรับการรายงานผล การทดลองนั้น จะเปรียบเทียบค่าที่ได้ตามทฤษฎีในรูปร้อยละ ซึ่งจะได้ความสัมพันธ์ดังนี้

ความเข้มข้นของสารละลายและการเตรียมสารละลาย
สารละลาย ( Solution) คือ สารเนื้อเดียวที่มีสารตั้งแต่ 2 ชนิดขึ้นไปมารวมกัน ประกอบด้วยตัวทำละลายและตัวถูกละลาย ถ้าตัวถูกสารละลายและตัวทำละลายมีสถานะเดียวกันสารละลายที่มีปริมาณมากกว่าเป็นตัวทำละลาย แต่ถ้าสารทั้งสองมีสถานะแตกต่างกันสารที่มีสถานะเดียวกันกับสารละลายเป็นตัวทำละลาย
หน่วยของสารละลาย เป็นค่าที่แสดงถึงปริมาณของตัวละลายที่ละลายอยู่ในตัวทำละลายหรือในสารละลายนั้น วัดในรูปความเข้มข้นปริมาณตัวถูกละลายต่อปริมาณสารละลาย ( ยกเว้นหน่วยโมลต่อกิโลกรัม)
1. ร้อยละ
1.1 ร้อยละโดยมวล ( มวล / มวล) คือ ปริมาณมวลของตัวถูกละลายในมวลของสารละลาย 100 หน่วยมวล
1.2 ร้อยละโดยปริมาตร ( ปริมาตร / ปริมาตร) คือ ปริมาตรของตัวถูกละลายในสารละลายปริมาตร 100 หน่วยปริมาตร นิยมใช้กับสารละลายที่เป็นของเหลว เช่น สารละลายแอลกอฮอล์เข้มข้นร้อยละ 20 โดยปริมาตร หมายความว่าสารละลายนี้ 100 ลูกบาศก์เซนติเมตรจะมีแอลกอฮอล์ละลายอยู่ 20 ลูกบาศก์เซนติเมตร
1.3 ร้อยละมวลต่อปริมาตร คือ ปริมาณของตัวถูกละลายในปริมาตรของสารละลาย 100 หน่วยปริมาตร โดยทั่วไปถ้ามวลของตัวถูกละลายมีหน่วยเป็นกรัม ปริมาตรของสารละลายจะมีหน่วยเป็นลูกบาศก์เซนติเมตร และถ้ามวลของตัวถูกละลายมีหน่วยเป็นกิโลกรัม ปริมาตรของสารละลายจะมีหน่วยเป็นลูกบาศก์เดซิเมตรหรือลิตร หน่วยมวลและหน่วยปริมาตรต้องให้สอดคล้องกันด้วย
1.2 ร้อยละโดยปริมาตร ( ปริมาตร / ปริมาตร) คือ ปริมาตรของตัวถูกละลายในสารละลายปริมาตร 100 หน่วยปริมาตร นิยมใช้กับสารละลายที่เป็นของเหลว เช่น สารละลายแอลกอฮอล์เข้มข้นร้อยละ 20 โดยปริมาตร หมายความว่าสารละลายนี้ 100 ลูกบาศก์เซนติเมตรจะมีแอลกอฮอล์ละลายอยู่ 20 ลูกบาศก์เซนติเมตร
1.3 ร้อยละมวลต่อปริมาตร คือ ปริมาณของตัวถูกละลายในปริมาตรของสารละลาย 100 หน่วยปริมาตร โดยทั่วไปถ้ามวลของตัวถูกละลายมีหน่วยเป็นกรัม ปริมาตรของสารละลายจะมีหน่วยเป็นลูกบาศก์เซนติเมตร และถ้ามวลของตัวถูกละลายมีหน่วยเป็นกิโลกรัม ปริมาตรของสารละลายจะมีหน่วยเป็นลูกบาศก์เดซิเมตรหรือลิตร หน่วยมวลและหน่วยปริมาตรต้องให้สอดคล้องกันด้วย
2. โมลาริตี หรือโมลต่อลูกบาศก์เดซิเมตร ( mol/dm 3 หรือ mol/l) เป็นหน่วยที่บอกจำนวนโมลของตัว ถูกละลายในสารละลาย 1 ลูกบาศก์เดซิเมตร หน่วยความเข้มข้นเป็นโมลต่อลูกบาศก์เดซิเมตรอาจเรียกย่อได้เป็นโมลาร์ (Molar) ใช้สัญลักษณ์ M
3. โมแลลิตี หรือ โมลต่อกิโลกรัม (mol/kg) เป็นหน่วยที่บอกจำนวนโมลของตัวถูกละลายที่ละลาย ในตัวทำละลาย 1 กิโลกรัม จึงมีหน่วยเป็น mol/kg หรือเรียกว่า โมแลล ( Molal) ใช้สัญลักษณ์ m
4. เศษส่วนโมล ( Mole fractions) คือ สัดส่วนจำนวนโมลของสารองค์ประกอบหนึ่งต่อจำนวนโมลรวม ของสารทุกชนิดในสารละลาย ใช้สัญลักษณ์ X เช่น สารละลายชนิดหนึ่งประกอบด้วยสาร A a mol, B b mol และ C c mol จะได้เศษส่วนโมลของสาร A, B และ C ดังนี้
เศษส่วนโมลของสาร A (X A) = a / ( a + b + c )
เศษส่วนโมลของสาร B (X B) = b / ( a + b + c )
เศษส่วนโมลของสาร C (X C) = c / ( a + b + c )
ผลรวมของเศษส่วนโมลของสารองค์ประกอบทั้งหมดคือ XA + XB + XC มีค่าเท่ากับ 1 และเมื่อนำค่าเศษส่วนโมลของแต่ละสารมาคูณด้วยร้อย จะได้ความเข้มข้นในหน่วยร้อยละโดยมวลของสารนั้น
ร้อยละโดยมวลของสาร A = เศษส่วนโมลของสาร A * 100
ร้อยละโดยมวลของสาร B = เศษส่วนโมลของสาร B * 100
ร้อยละโดยมวลของสาร C = เศษส่วนโมลของสาร C * 100
5. ส่วนในล้านส่วน ( parts per million; ppm) เป็นหน่วยที่บอกมวลของตัวถูกละลายที่ละลายอยู่ในสารละลาย 1 ล้านหน่วยมวลเดียวกัน ซึ่งเป็นหน่วยความเข้มข้นของสารละลายที่เจือจางมาก ๆ หรืออาจใช้แสดงปริมาณของสิ่งเจือปนที่มีอยู่ในสารเคมีที่บริสุทธิ์ต่าง ๆ เช่น สารละลายโพแทสเซียมไนเตรตเข้มข้น 2 ppm หมายความว่ามีโพแทสเซียมไนเตรตเป็นตัวละลาย 2 ส่วน (กรัม) ละลายอยู่ในสารละลาย 1 ล้านส่วน ( กรัม) หรือ 106 กรัม

ในกรณีที่สารละลายเจือจางมากๆ มวลของสารละลายมีค่าน้อยมากเมื่อเทียบกับมวลของตัวทำละลาย ทำให้มวลของสารละลายมีค่าใกล้เคียงกันมากกับมวลของตัวทำละลายจนถือว่าเท่ากันได้
การเตรียมสารละลาย
การเตรียมสารละลายนั้นสามารถทำได้เป็น 2 วิธีใหญ่ คือ การเตรียมจากการละลายของสารบริสุทธิ์ และเตรียมจากสารละลายเดิม โดยทำให้เจือจางลง ซึ่งจะมีกรรมวิธีในการเตรียมที่แตกต่างกันไป แต่ถ้าเตรียมอย่างถูกต้องก็จะได้สารละลายที่มีความเข้มข้นตามต้องการได้เแม่นยำ นักเรียนคิดว่าการเตรียมสารละลายเตรียมได้จากสารบริสุทธิ์โดยตรง หรือเตรียมจากการเจือจางสารละลายเดิมที่มีอยู่สองวิธีนี้มีความแตกต่างกันอย่างไร
ในการคำนวณปริมาณสารที่ใช้เตรียมสารละลายนั้น สิ่งที่จำเป็นต้องทราบ คือปริมาณตัวละลายที่ต้องการ และปริมาณของสารละลายทั้งหมด
ตัวอย่าง ในกรณีนี้ ต้องการ โพแทสเซียมเปอร์แมงกาเนต (KMnO 4) เข้มข้น 0.005 โมลาร์ ปริมาตร 250 cm 3
ซึ่งความเข้มข้น 0.005 โมลาร์นั้น หมายความว่า สารละลาย 1,000 cm 3 จะมีโพแทสเซียมเปอร์แมงกาเนตอยู่ 0.005 โมล
ดังนั้นสารละลาย 250 cm 3 ก็จะมีโพแทสเซียมเปอร์แมงกาเนตอยู่ 0.005 x 250 = x โมล
โพแทสเซียมเปอร์แมงกาเนตมีมวลโมเลกุล = 158 แสดงว่า โพแทสเซียมเปอร์แมงกาเนต 1 โมล จะหนัก 158 กรัม
ต้องการ X โมล ต้องชั่งมา X กรัม
การเจือจางสารละลายนั้นต้องการโพแทสเซียมเปอร์แมงกาเนต 0.001 โมล ปริมาตร 100 cm 3
สารละลาย 0.001 โมล แสดงว่า สารละลาย 1,000 cm 3 มีโพแทสเซียมเปอร์แมงกาเนตละลายอยู่ 0.001 โมล
ในสารละลาย 100 cm 3 มีโพแทสเซียมเปอร์แมงกาเนตละลายอยู่ 100 x 0.001 / 1,000 = y โมล
สารละลาย 0.005 โมล ของโพแทสเซียมเปอร์แมงกาเนตแสดงว่า มีโพแทสเซียมเปอร์แมงกาเนต 0.005 โมล ใน สารละลาย 1,000 cm 3 ถ้าต้องการ y โมล ต้องใช้สารละลาย 1,000 y / 0.005 = ? cm 3

สมบัติคอลลิเกทีฟของสารละลาย
สารละลายเป็นสารเนื้อเดียวที่ได้จากการผสมสารบริสุทธ์ตั้งแต่ 2 ชนิดขึ้นไปเข้าด้วยกัน ถ้าสารที่นำมาผสมกันมีสถานะเดียวกันจะถือว่าสารที่มีปริมาณมากที่สุดเป็นตัวทำละลาย ส่วนสารที่มีปริมาณน้อยกว่าเป็นตัวละลาย จุดเดือดของสารละลายสูงกว่าตัวทำละลายบริสุทธิ์ และจุดหลอมเหลวของสารละลายต่ำกว่าตัวทำทำละลายบริสุทธิ์ และถ้าสารละลายที่มีความเข้มข้นในหน่วยโมลต่อกิโลกรัมเท่ากัน จะมีจุดเดือดและจุดหลอมเหลวเท่ากัน โดยที่ตัวละลายจะเป็นสารใดก็ได้แต่ต้องเป็นสารที่ระเหยยากและไม่แตกตัวเป็นไอออน ส่วนสารละลายที่มีความเข้มข้นต่างกัน แม้จะมีตัวทำละละายชนิดเดียวกันก็มีค่าจุดเดือดและจุดหลอมเหลวไม่เท่ากัน
สูตรเกี่ยวกับสารละลายที่มีสมบัติคอลลิเกตีฟ
1. จุดเดือด

= จุดเดือดของสารละลาย - จุดเดือดของตัวทำละลาย (องศาเซลเซียส)
K b = ค่าคงที่ของการเพิ่มขึ้นของจุดเดือดของสารละลาย ( องศาเซลเซียส /mol/kg)
m = ความเข้มข้นของสารละลาย ( mol/kg)
m 1 = มวลตัวถูกละลาย ( g)
m 2 = มวลของตัวทำละลาย ( g)
MW 1 = มวลโมเลกุลของตัวถูกละลาย
2. จุดหลอมเหลว ( หรือจุดเยือกแข็ง)

= จุดเยือกแข็งของตัวทำละลาย - จุดเยือกแข็งของสารละลาย (องศาเซลเซียส)
K f = ค่าคงที่ของการลดลงของจุดเยือกแข็งของสารละลาย ( องศาเซลเซียส /mol/kg)
3. สารละลายชนิดเดียวกันมีความเข้มข้นเท่ากัน จุดเดือดและจุดเยือกแข็งสัมพันธ์กันดังนี้

รวมสูตรการคำนวณสารละลาย
1. ร้อยละโดยมวลของตัวถูกละลาย
| |
2. ร้อยละโดยปริมาตรของตัวถูกละลาย
| |
3. ร้อยละโดยมวลต่อปริมาตรของตัวถูกละลาย
| |
4. mol/dm 3
| |
5. mol/kg
| |
6. สารละลายที่มีความเข้มข้น C mol/dm 3 จำนวน V dm 3 จำนวนโมลของตัวถูกละลาย n mol
 | |
7. สารละลายที่มีความเข้มข้น C mol/dm 3 จำนวน V dm 3 จำนวนโมลของตัวถูกละลาย n mol
 | |
8. การเปลี่ยนหน่วยสารละลายจากหน่วย ร้อยละ -----------> mol/dm 3



| |
9. การเตรียมสารละลายเจือจางโดยการเติมน้ำ
โมลของตัวถูกละลายก่อนเติมน้ำ = โมลของตัวถูกละลายหลังเติมน้ำ
สารละลาย C 1 mol/dm 3 จำนวน V 1 cm 3 เติมน้ำเป็นสารละลาย C 2 mol/dm 3 จำนวน V >2 cm 3 | |
10. การเตรียมสารละลายโดยการผสมสารละลายชนิดเดียวกันความเข้มข้นต่างกัน แต่ปริมาตรที่ใช้ต่างกัน
| |





ไม่มีความคิดเห็น:
แสดงความคิดเห็น